Exploring Kolmogorov-Arnold Networks (KANs)

Last updated on 
Exploring Kolmogorov-Arnold Networks (KANs)

Introduction

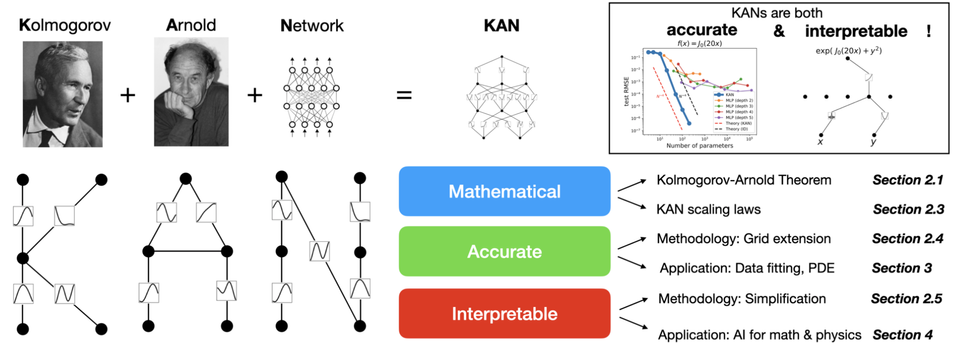
The Kolmogorov-Arnold Network (KAN) represents a significant advancement in neural network architecture, leveraging the powerful Kolmogorov-Arnold representation theorem. This innovative approach, pioneered by researchers from MIT, Caltech, Northeastern University, and the NSF Institute for AI and Fundamental Interactions, introduces a new paradigm in neural networks that promises enhanced flexibility and theoretical robustness.

The Essence of KANs

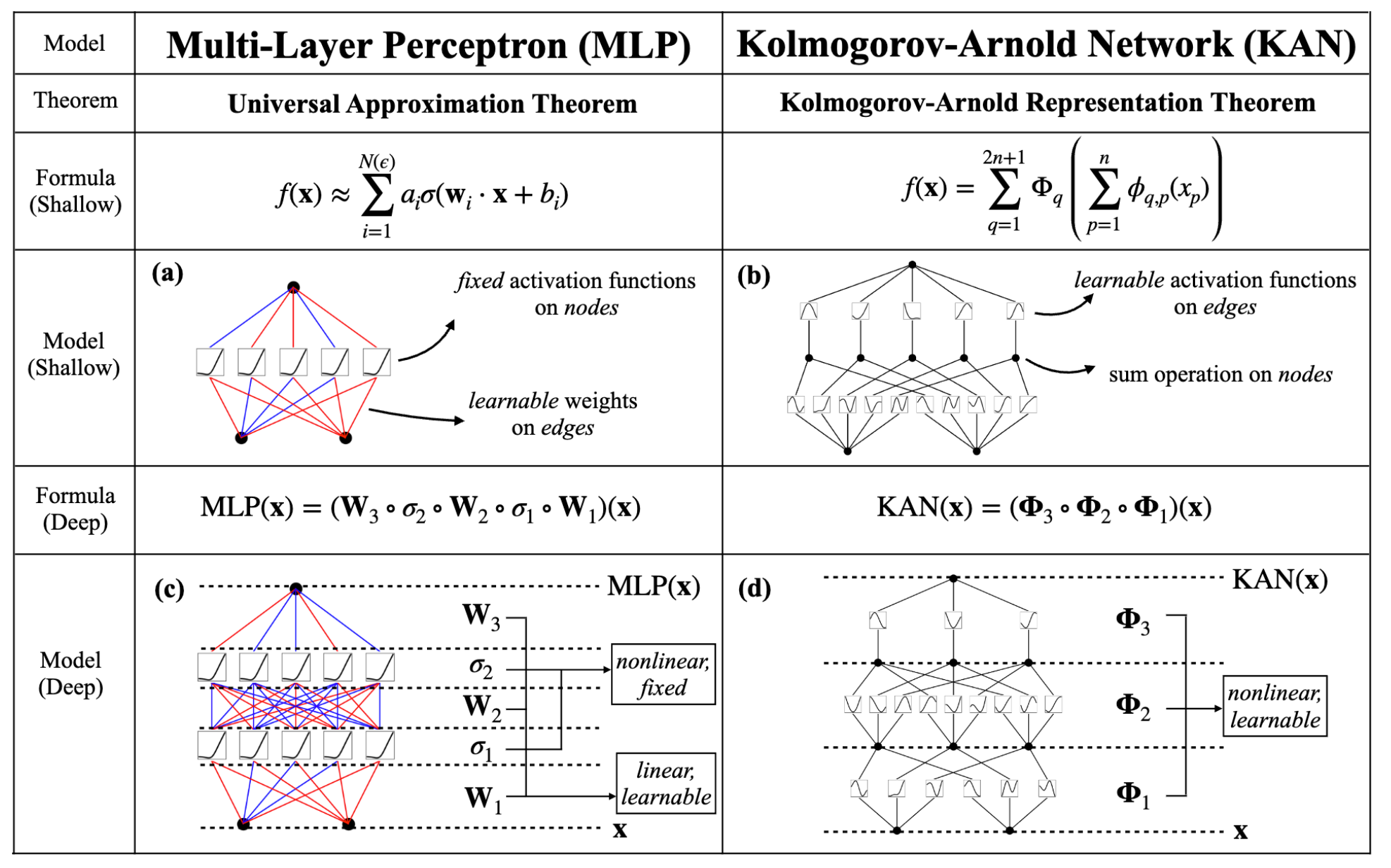
At the core of KANs lies the Kolmogorov-Arnold theorem, which states that any multivariate continuous function can be decomposed into a finite composition of continuous univariate functions and the binary operation of addition. This foundational principle enables KANs to employ learnable activation functions on the edges (weights) of the network, rather than on the nodes as seen in traditional Multi-Layer Perceptrons (MLPs).

KAN Architecture and Learning Process

The architecture of KANs involves the following steps:

  1. Identifying suitable univariate functions to approximate the target function.
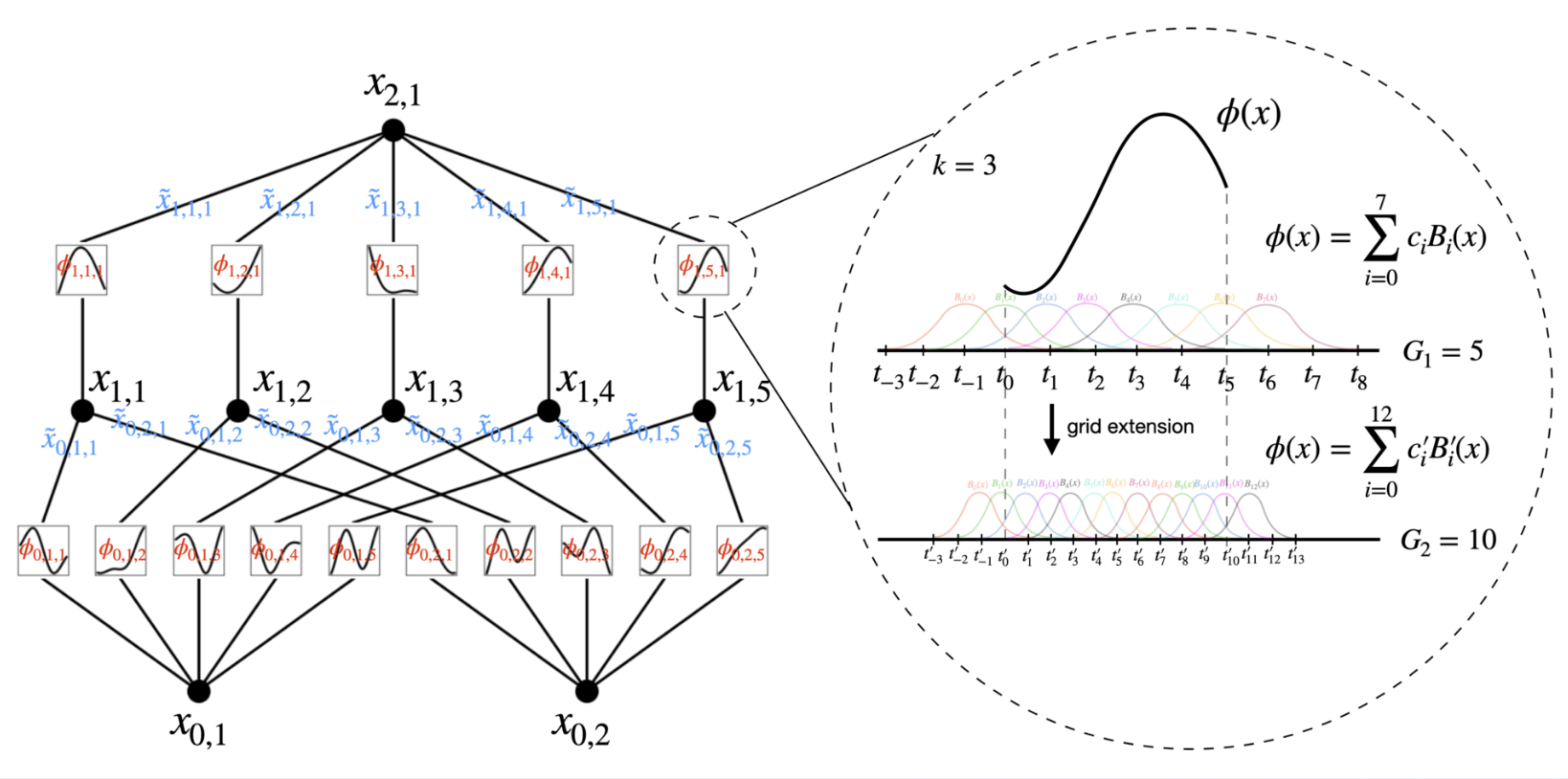
  2. Parameterizing each univariate function as a B-spline curve.
  3. Extending the network's depth and width, drawing an analogy with MLPs, by stacking additional layers.

This design allows KANs to overcome the limitations of simpler networks, enabling them to approximate any function with smooth splines by generalizing and deepening the network structure.

Architecture of KANs

Advantages Over MLPs

KANs offer several key advantages over traditional MLPs:

  • Flexibility in Activation Functions: Unlike MLPs, which typically use fixed activation functions, KANs utilize learnable activation functions on the edges. This feature enhances the network’s ability to adapt and optimize during training.
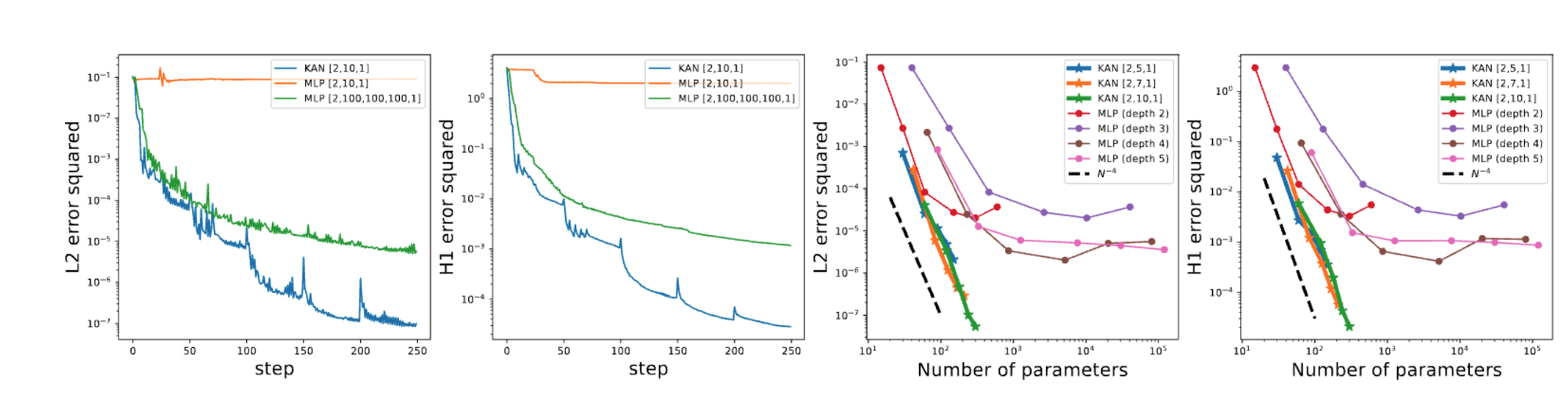
  • Parameter Efficiency: KANs generally require fewer parameters than MLPs, which not only reduces the computational load but also improves generalization.
  • Grid Extension for Accuracy: KANs can refine their spline grids for greater accuracy without retraining the entire model from scratch. This fine-graining capability allows for better performance tuning compared to the fixed structure of MLPs.

Implementation and Training

KANs can be implemented using a two-layer network with the original Kolmogorov-Arnold representation corresponding to a shape of [n, 2n+1, 1]. All operations within this framework are differentiable, enabling the use of backpropagation for training. Furthermore, KANs can scale efficiently by adding more layers, maintaining a balance between network complexity and performance.

Case Study: Solving PDEs

A practical example of KANs' application is in solving partial differential equations (PDEs). By using splines to approximate the solution, KANs can efficiently handle problems such as the Poisson equation with zero Dirichlet boundary conditions, showcasing their potential in complex mathematical and engineering tasks.

The PDE example: L2 squared and H1 squared losses between the predicted solution and ground truth solution. First and second: training dynamics of losses. Third and fourth: scaling laws of losses against the number of parameters. KANs converge faster, achieve lower losses, and have steeper scaling lawsthan MLPs.

Conclusion

Kolmogorov-Arnold Networks mark a significant step forward in the field of neural networks, combining theoretical rigor with practical efficiency. As research continues, we can anticipate further refinements and broader applications of KANs in various domains, from AI to computational mathematics.

Authors

Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, and Max Tegmark

References For a detailed exploration of KANs and their theoretical underpinnings, the full research can be accessed on ArXiv.