A Mazing Transformer

Last updated on Aug 22, 2023

Photo generated by DALL-E 2

Transformers, as initially introduced by Vaswani et al. in the seminal paper "Attention is All You Need" [1], represent a class of remarkably efficient architectures designed for processing sequential inputs. While their origins lie in language modeling and linguistic tasks, the profound impact of Transformers has extended well beyond these domains. Their remarkable performance in diverse fields, including vision and audio processing, has elevated them into versatile instruments within the realm of machine learning research and practical applications.

Scaled Dot-Product Attention

The fundamental concept underpinning attention in machine learning is the computation of a weighted average across a sequence of inputs. In the context of Transformers, this weighted average is accomplished through the utilization of the scaled dot-product attention mechanism. This mechanism consists of three pivotal components: Keys (\(K\)), Queries (\(Q\)), and Values (\(V\)). Within each attention layer, each token within the input sequence undergoes transformations, resulting in query, key, and value vectors, facilitated by three distinct linear projections. Importantly, since these transformations are independant among the input tokens, they are well fitted to parallel processing. The dot product, representing the degree of similarity, is computed for all combinations of queries and keys, thereby establishing the asymmetric attention weight for each token concerning the others. Subsequently, these weights will be applied when combining the value vectors:

\[\begin{align}\text{Attention}(Q,K,V) = \text{softmax}\left(\frac{QK^T}{\sqrt{d_k}}\right)V,\end{align}\]

Where \(d_k\) is the size (number of dimensions) of the keys and query vectors.

Multiple attention heads are usually used to make the attention more varied at each layer instead of using just one. In these multi-head attention layers, each "head" has its own set of trainable parameters (like projection weights). These heads' results are then combined and transformed using a linear projection:

\[\begin{align}&\text{MultiHead}(Q,K,V) = \\&\text{Concat}(\text{head}_1,...,\text{head}_h)W^O,\end{align}\]

\[\begin{align}\text{head}_i = \text{Attention}(QW_i^Q,KW_i^K,VW_i^V),\end{align}\]

where

\[\begin{align}W_i^Q &\in \mathbb{R}^{d_{model}\times d_k},\\W_i^K &\in \mathbb{R}^{d_{model}\times d_k},\\W_i^V &\in \mathbb{R}^{d_{model}\times d_v},\\W^O &\in \mathbb{R}^{hd_{v}\times d_{model}},\end{align}\]

\(d_{model}\) is the dimension of output vectors in all encoder and decoder layers.

Encoders and Decoders

The original transformers architecture was first designed for language translation, where it handles two sets of sequences: the source language to be understood and the target language to be generated. In this context, encoder modules analyze and create a representation of the source language, while decoder modules handle the target language. The decoder also has access to the information from the encoder to produce an output suitable for generating the translated sentence in the target language. Both encoder and decoder modules employ multi-head attention mechanisms.

In the upcoming sections, we'll illustrate how transformers can be employed to solve a maze. In this scenario, an image of the maze is fed as input, and the transformer generates a sequence of moves as the output. Solving a maze in this way involves vision and action which demonstrates that transformers are not limited to language tasks alone; they exhibit versatility across various types of sequences!

Problem Definition

Each maze is a 5x5 grid of random tiles. Each tile is a 5x5 array. The tiles can be 0-4 directional (any rotation):

Possible number of directions for a tile

Dark (0) and light (1) colors represent blocked and open areas, respectively. To distinguish the start and end tiles, the central pixel value is set to 2 (cyan) and 3 (black):

The goal is to start from the "start" tile and generate a sequence of moves that eventually reaches the "end" tile. There are 6 types of moves: STOP (0), UP (1), RIGHT (2), DOWN (3), LEFT (4), START (5). The amount of displacement is one tile per move (except the STOP and START moves). START and STOP are indicators of the beginning and end of the solution, respectively.

For instance, here is the solution move sequence to the maze sample shown above:

start,up,right,down,right,down,right,up,right,stop

Data Generation and Dataset

Here are the steps for generating a data sample:

Create an empty grid.
Choose a path length between 2 and 18 randomly (L).
Choose a random tile as the "start" tile.
Make a random walk starting from the "start" tile and perform at most L steps. The path should not pass itself or the boundaries of the grid.
Append START and STOP to the beginning and end of the move sequence, respectively.
Overlay a random grid on top of the generated random walk.
If there exists a shorter path between the "start" and "end" tiles, replace the random walk with a move sequence that follows the shortest path.
Store the grid as the input and the sequence of moves (i.e. random walk) as the output.

The final dataset contains 10000 training and 1000 validation samples. We make sure that the two sets do not share any sample.

Transformer Architecture

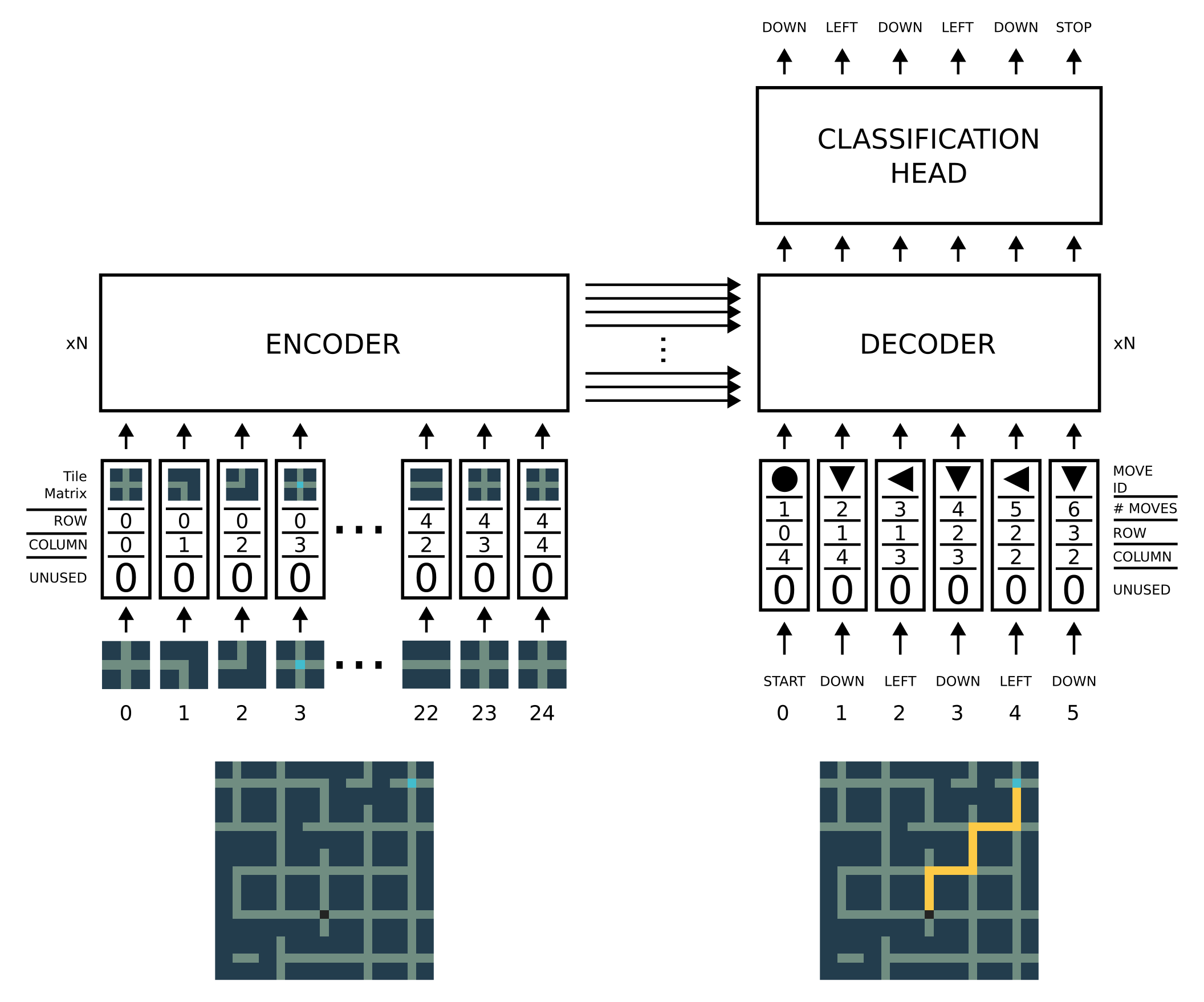
To solve the maze, we use a transformer architecture with both encoder and decoder modules.

The input to the encoder is the sequence of maze tiles. Each tile is represented as a feature vector of size 32. The first 25 elements contain the flattened tile matrix. The row and column indices of the tile are stored at indices 26 and 27, respectively. The rest of the vector is set to 0.

The input to the decoder is the sequence of moves each represented by a vector of size 32. The first element of the vector holds the integer id of the last move (0-5). The second element represents the number of moves so far. The third and the fourth elements represent the current tile row and column indices, respectively.

The outputs of the decoder are sent to a fully connected layer to decide the next move in the sequence.

Training

During the training, the whole input maze and output moves are respectively fed into the first encoder and first decoder. Decoders use target mask to prevent the leak of the information from the future. In the end, Cross Entropy loss is used for the optimization.

Testing

We use a validation set to evaluate the classification accuracy after each training epoch. When the training is done, we reload the network with best validation accuracy and use it with the test maze samples.

For each test maze, we start by giving the whole maze to the encoder. Then, we create the first output vector for the decoder by setting the move id to START, the move count to 1, and the row and column indices to those corresponding to the "start" tile. Every time we run the network, the classification of the last token will be considered as the next move. We then iteratively append the predicted moves (together with the updated move counter and current row and column indices) to the sequence fed to the decoder to obtain the future moves. We will stop the process when the network outputs an invalid move (i.e. crossing the grid boundaries or blocked areas) or the STOP move.