Catmull-Clark's algorithm

Last updated on 
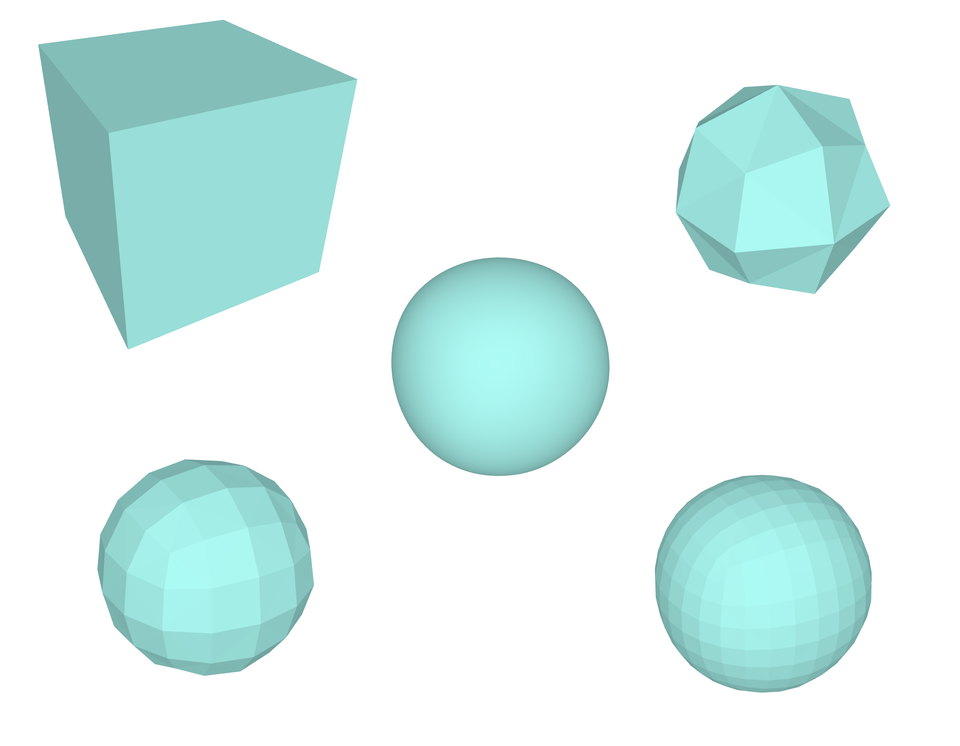
Catmull-Clark's algorithm
Catmull-Clark applied to the cube.

Meshes

Meshes are massively used in 3D modelling for animation or design, the representation is simple.

  • Vertices: points in space.
  • Edges: a straight line between vertices.
  • Faces: a surface delimited by edges.

Meshes are easy to manipulates, and many tools exist to use them. In the heart of every 3D images there are meshes.

However there is an intrinsic limit to the use of meshes: the limit of polygons. Many real surfaces are smooth. Meshes, by definition, are an amalgamation of small flat surfaces with sharp edges. One way to solve this problem is to use normal vectors for computing light effects and hiding the sharp edges. Sadly the edges can still be seen on the side.

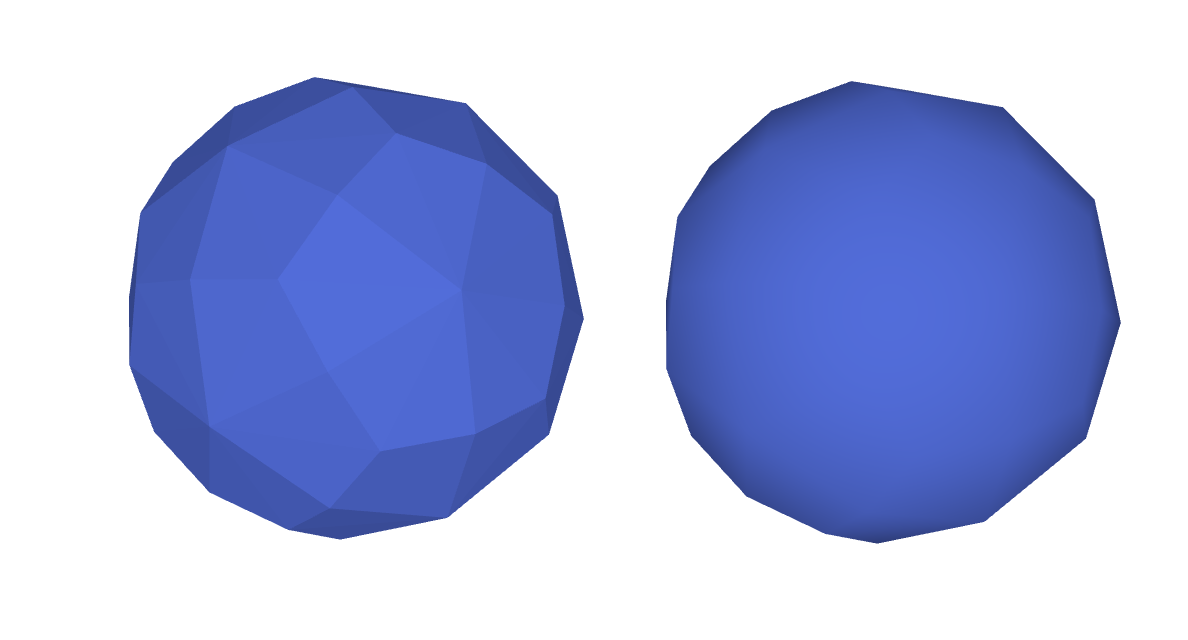
A sphere, with no normal vectors (left), with normal vectors (right). Observe the edges visible on the side.

Generally to solve this issue one increase the number of polygons of the object.

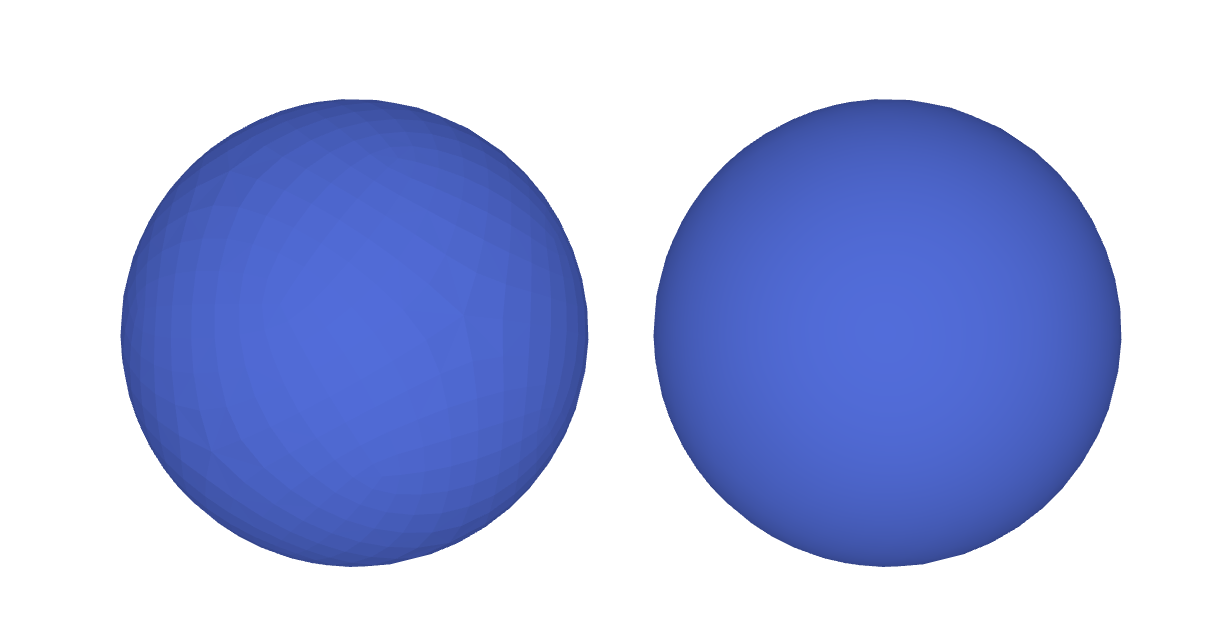
A better approximation of the sphere.

However it is not always easy to increase the number of polygons, as the general shape of the object might not been known. The goal of Catmull-Clark's algorithm is to define a relatively natural smooth surface and give good approximations of this surface.

Catmull-Clark

This algorithm subdivides each face of the original mesh. It first create one vertex per face, then one vertex per edge, move the original vertices, cut original edge into two, add new edges, then cut original faces using the newly created edges.

We start from a mesh, call its vertices its original vertices.

A simple mesh

For each face add a face vertex at the center (barycenter of vertex incident to the face).

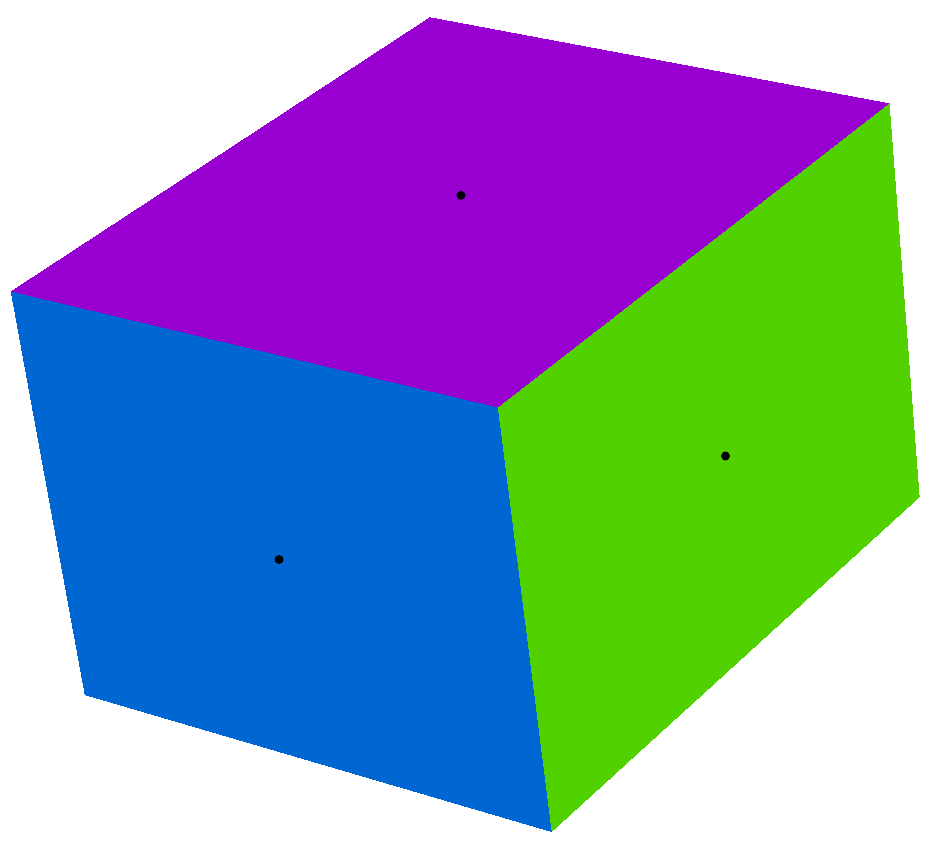
Mesh with the face vertices (black). The vertices are on the corresponding faces.

For each edge add an edge vertex, at the barycenter of adjacent face's vertices and vertices incident to the edge.

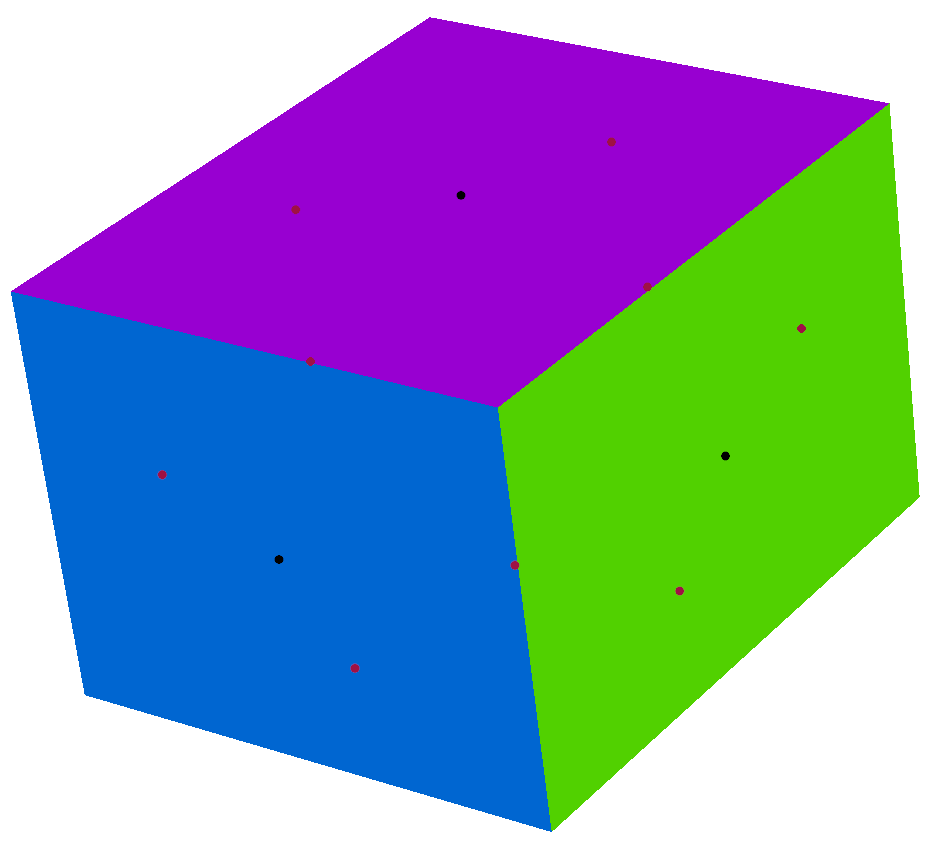
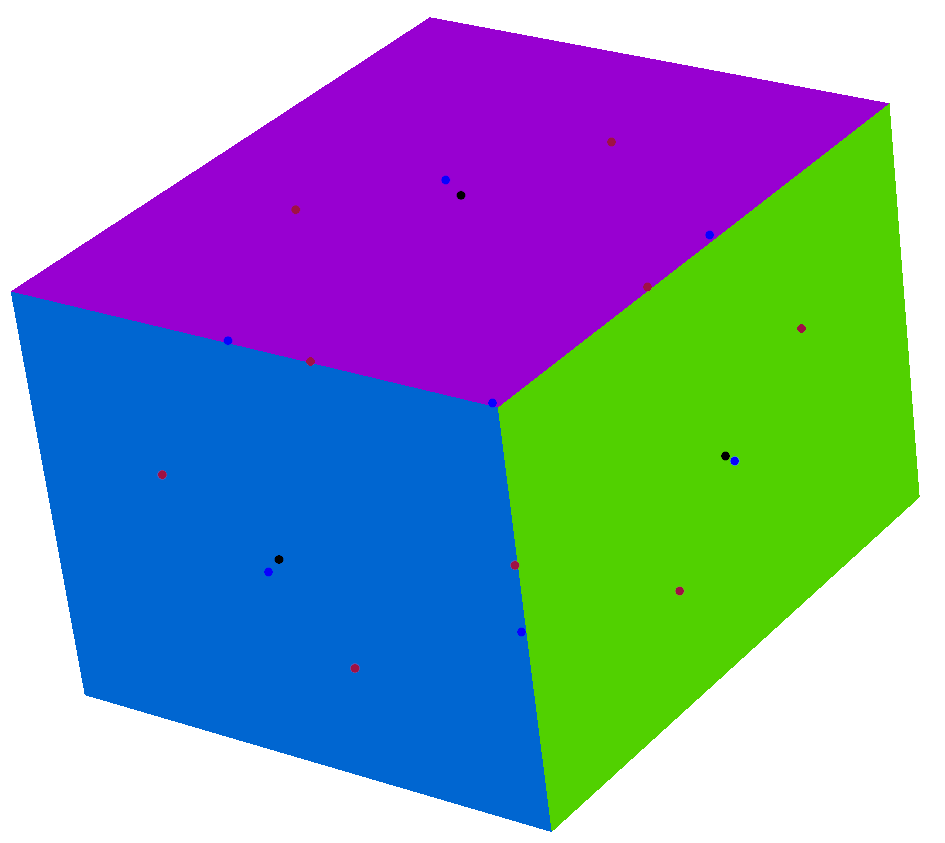
Mesh with face vertices and edge vertices (red). The edge vertices are inside the mesh.

Move the original vertex toward the 'center'. The new coordinates of original vertex V is (F+2E+(n-2)V)/n.

    Where:
  • n is the number of faces incident to V.
  • F is the average of all new face vertices of faces incident to V.
  • E is the average of all midpoints edges incident to V.

Mesh with moved vertex (blue), they are inside the mesh.
All our vertices!

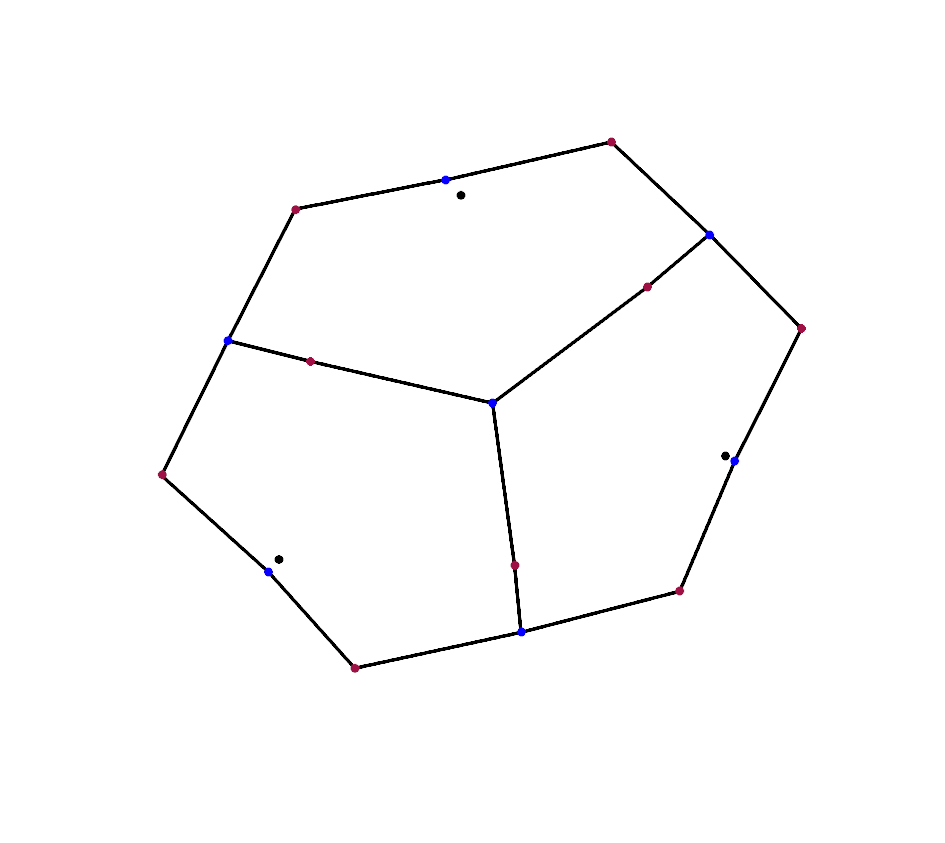
Cut original edges into two going from a moved original vertex to an edge vertex.

The cut edges

Add edges from each face vertex to all adjacent edges' vertices.

All our new edges.

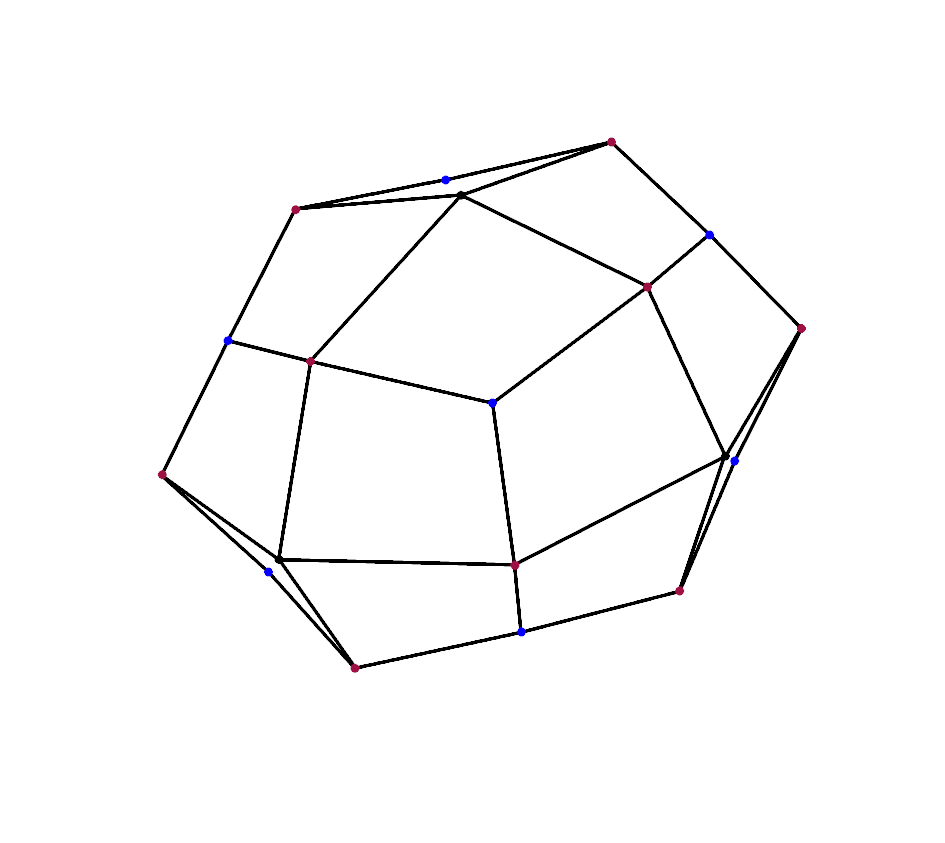
Finally we cut our original faces with the new edges.

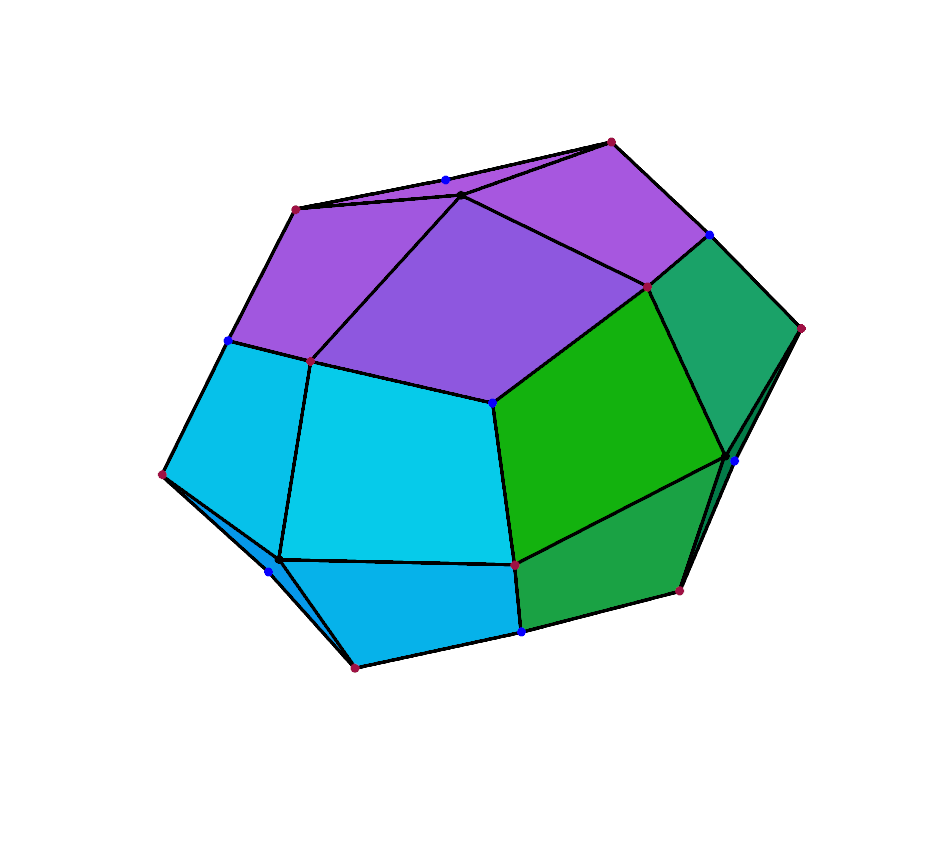
Here is a visualization of the whole process.

All Catmull-Clark steps

Applying Catmull-Clark algorithm to a mesh yields a converging sequence of surfaces. The limit is a nice smooth surface.

A converging sequence of Catmull-Clark meshes

References

  1. E. Catmull, J. Clark, Recursively generated B-spline surfaces on arbitrary topological meshes. Computer-Aided Design. 10 (6): 350 (1978).
  2. J. Stam, Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. Proceedings of the 25th annual conference on Computer graphics and interactive techniques - SIGGRAPH '98. pp. 395–404 (1998).
  3. Wikipedia: Catmull-Clark subdivision surface