SkinGAN Project using LaMa-Fourier

Goal
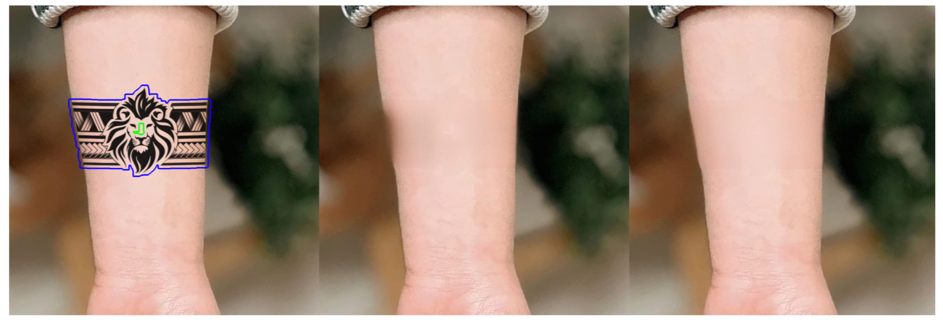
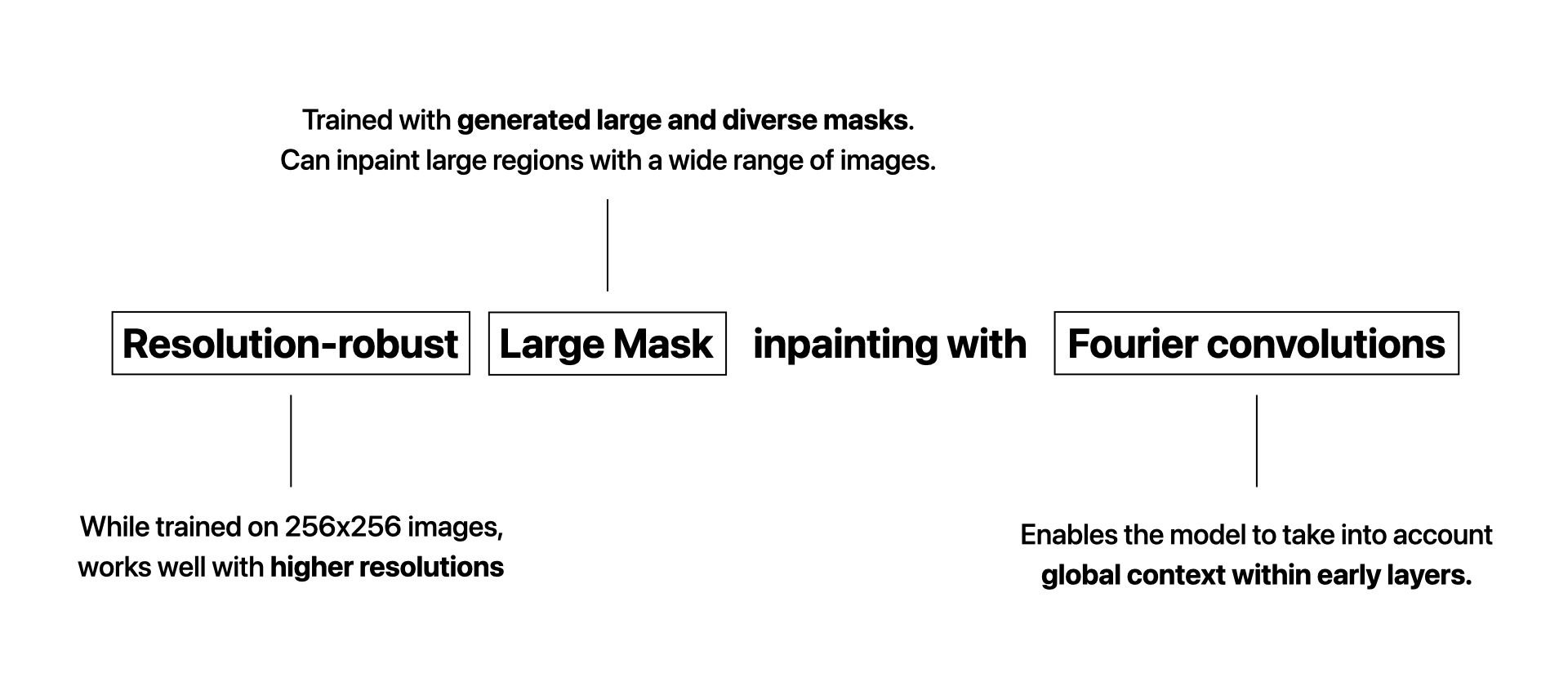
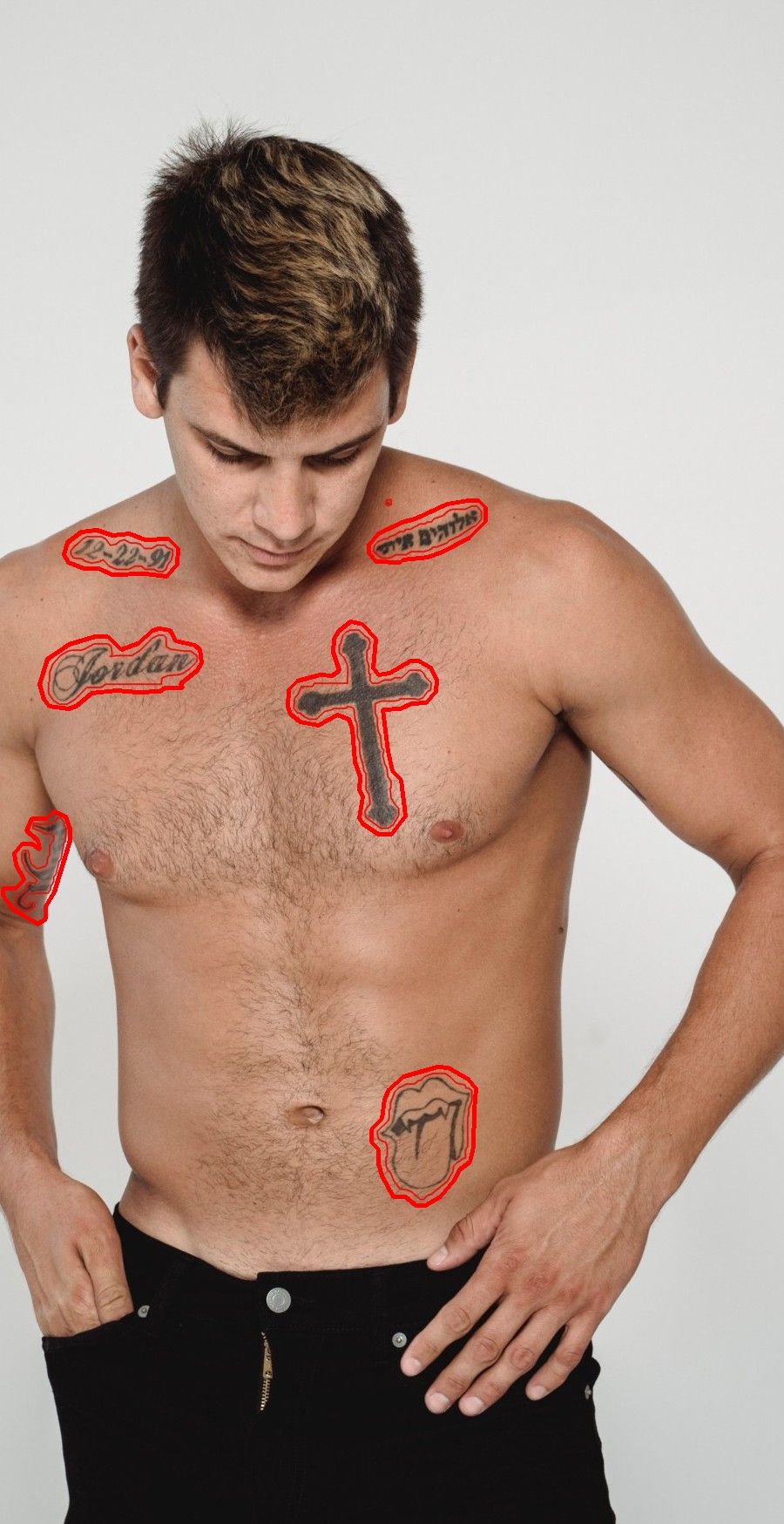
The goal of this project is to help protect the privacy of Belle customers by removing the tattoos that would enable them to be identified. Thus, we use AI to replace tattoos with realistic and relevant skin. Another interesting use case is the removal of acne. We chose a model called LaMa (large mask inpainting) for its performance when using large masks (SOTA in Nov. 2021), its light weight and its ability to generalize well to a much higher resolution.


Here's some examples of inpainting with LaMa-Fourier. Please click on an image in the gallery to enlarge it.
LaMa Overview
The problem with ConvNets
First, let's define the concept of Receptive Field (RF).
The RF of a output unit is the region in the input that produces that output unit.
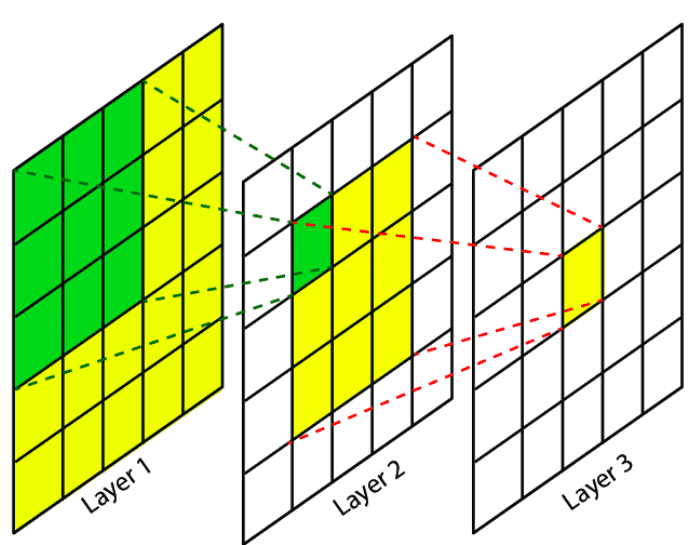
Similarly, the Effective RF (EFR) is the region that contains any input pixel with a non-negligible impact.
A regular convolution on a particular point will take into account its local neighborhood so a CNN needs a lot of layers in order to integrate information across the whole image. When using large masks and small kernels, the RF may fall into the masked region through several layers !

Existing approaches convolutional models have slowly-growing RFs, resulting in wasted computational resources and model parameters. Hence, to correctly inpaint wide and large missing parts of an image, a good architecture should have units with a RF as wide as possible and as soon as possible.
Global context within early layers with Fast Fourier Convolutions (FFC)
Fast Fourier Convolutions allows LaMa to acquire global context and to use information from all parts of the image, from the start, to inpaint masked regions.
Before moving on, let's remind the concept of Fast Fourier Transform (FFT) :
We use FFT to transform an image to the frequency (also called Fourier) domain and the Inverse Transform (IFFT) to retrieve the image in the spatial domain.
The reasoning behind FFC is the following :
- convolution in the spatial domain = conv. across the neighbors of the pixel
- convolution in the Fourier domain = conv. across the neighboring frequencies
- every value in the Fourier domain represents information about all the image
=> updating a single value in the Fourier domain affects all original data !

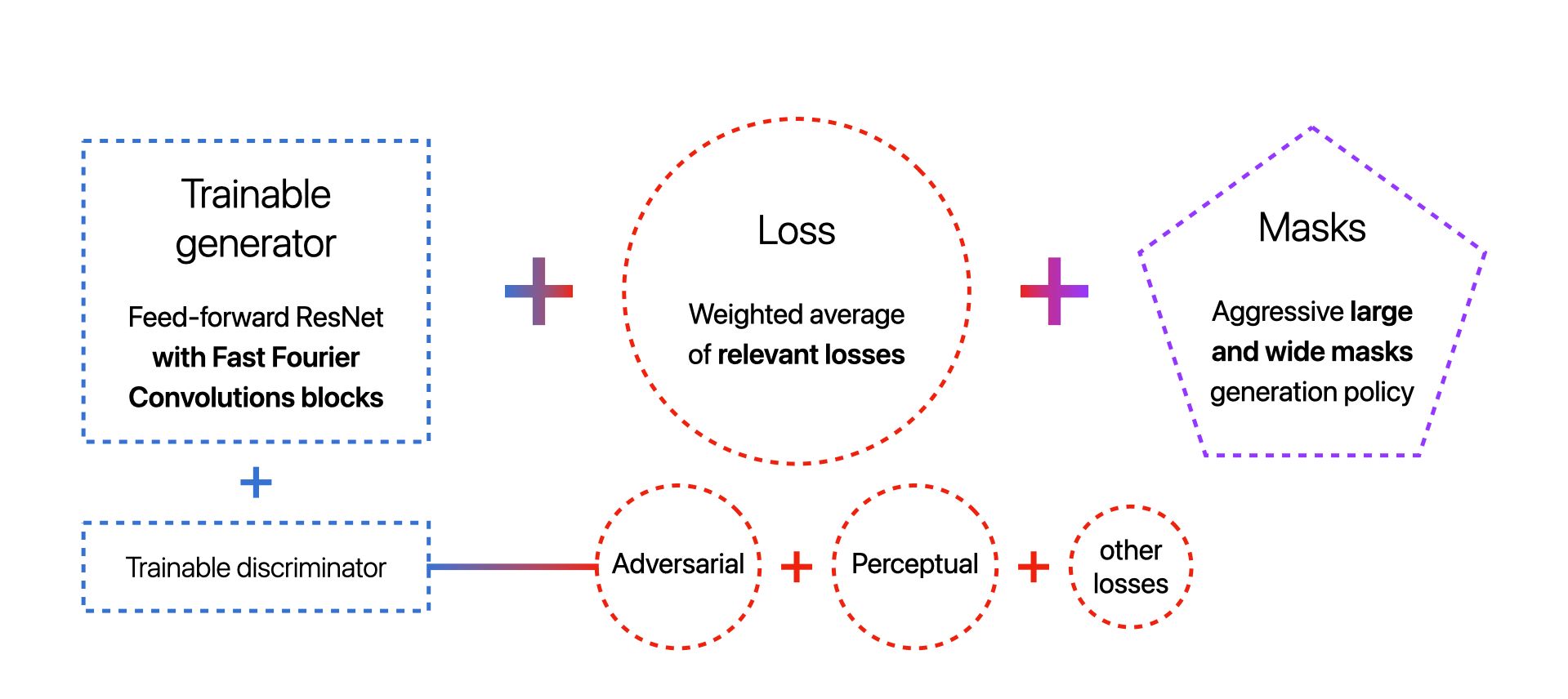
Generator with FFC
The generator is a feed-forward fully-convolutional neural network composed of a downscaling step followed by 9 FFC-based residual blocks (or 18 blocks for the deeper model), completed by an upscaling step.
It takes a 3D masked image stacked with the binary mask (a 4D tensor) as input and predicts an 3D inpainted image.
Here's a schema of the generator architecture, from the paper:

Now, let's detail, step by step, how the FFC operation works :
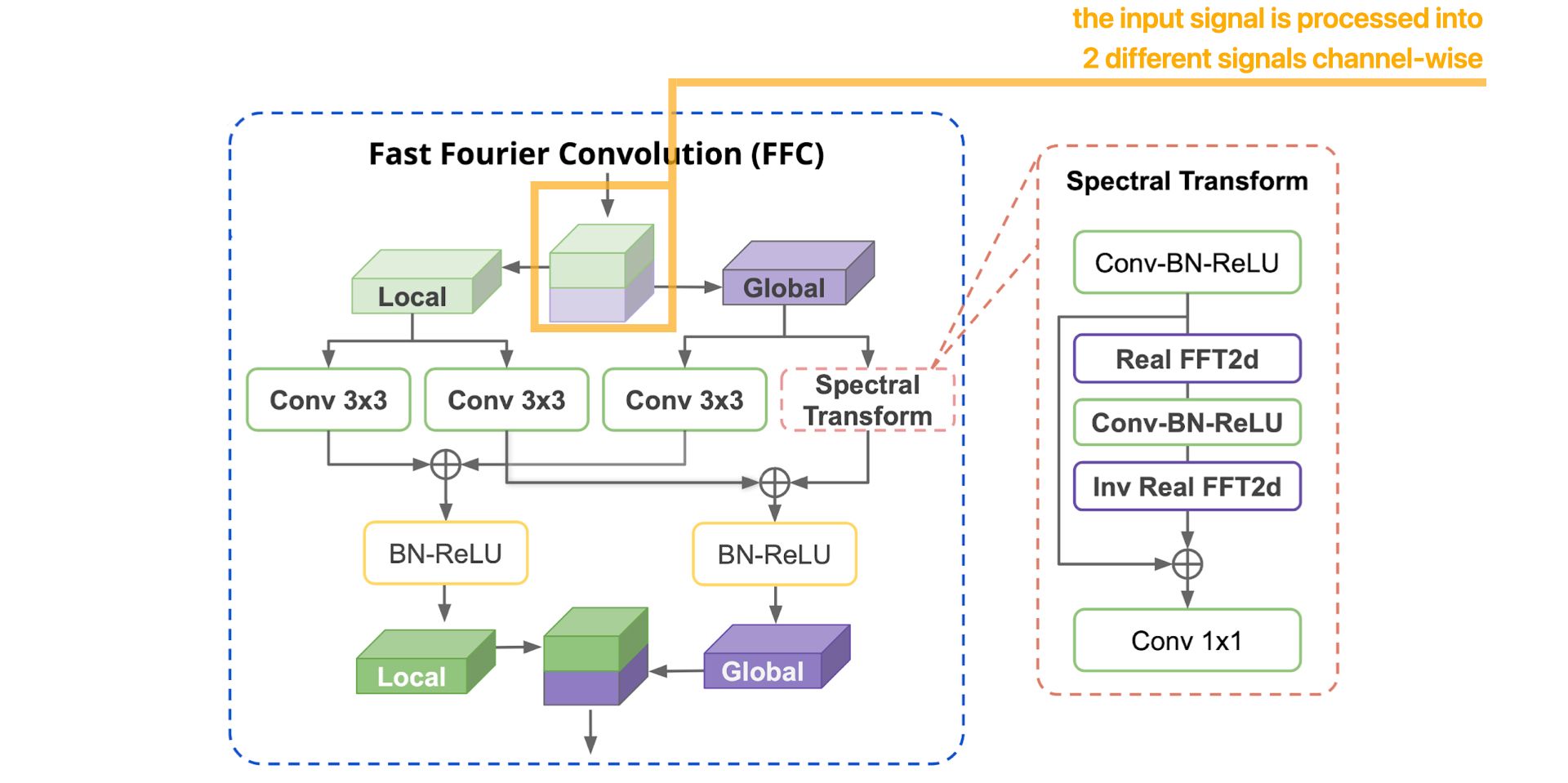
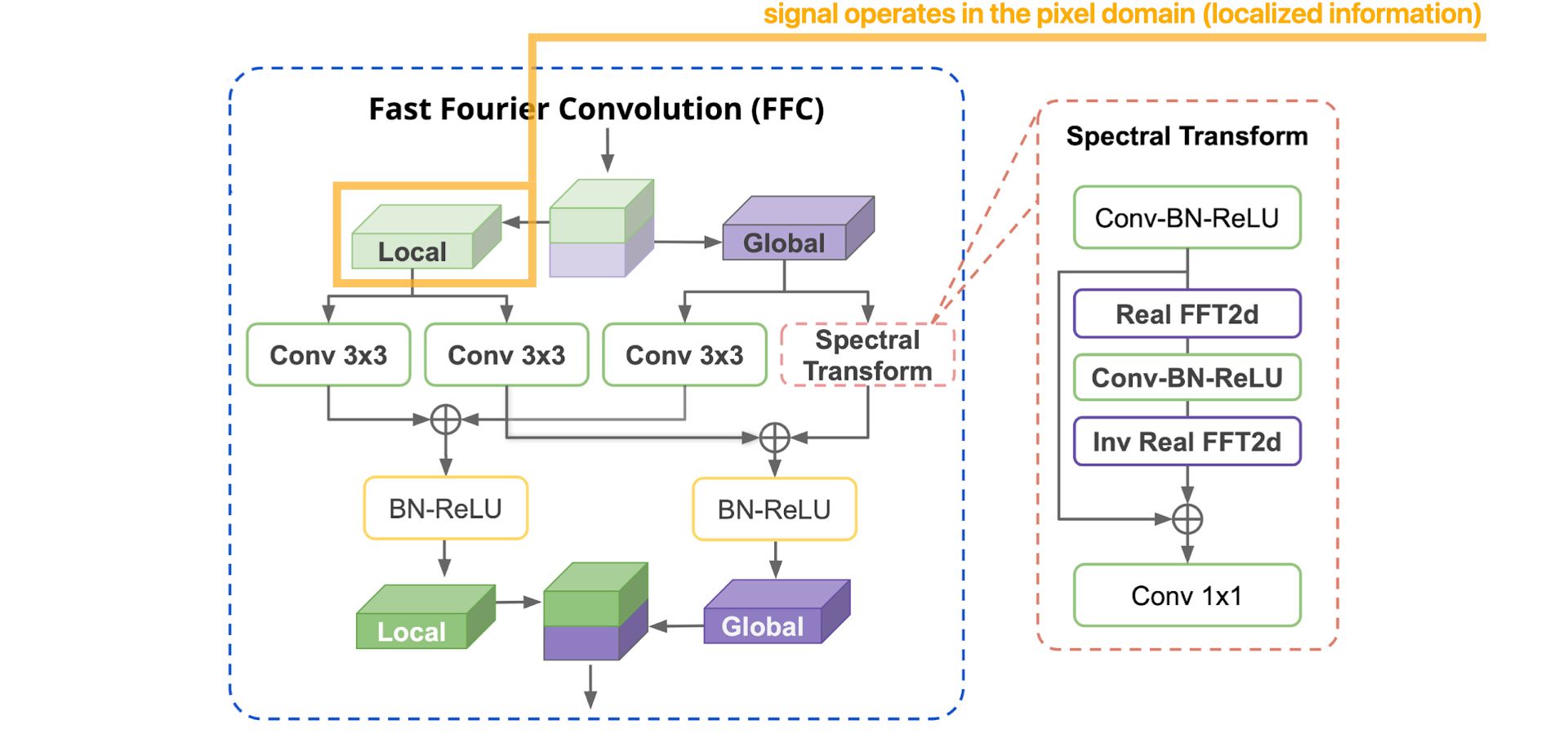
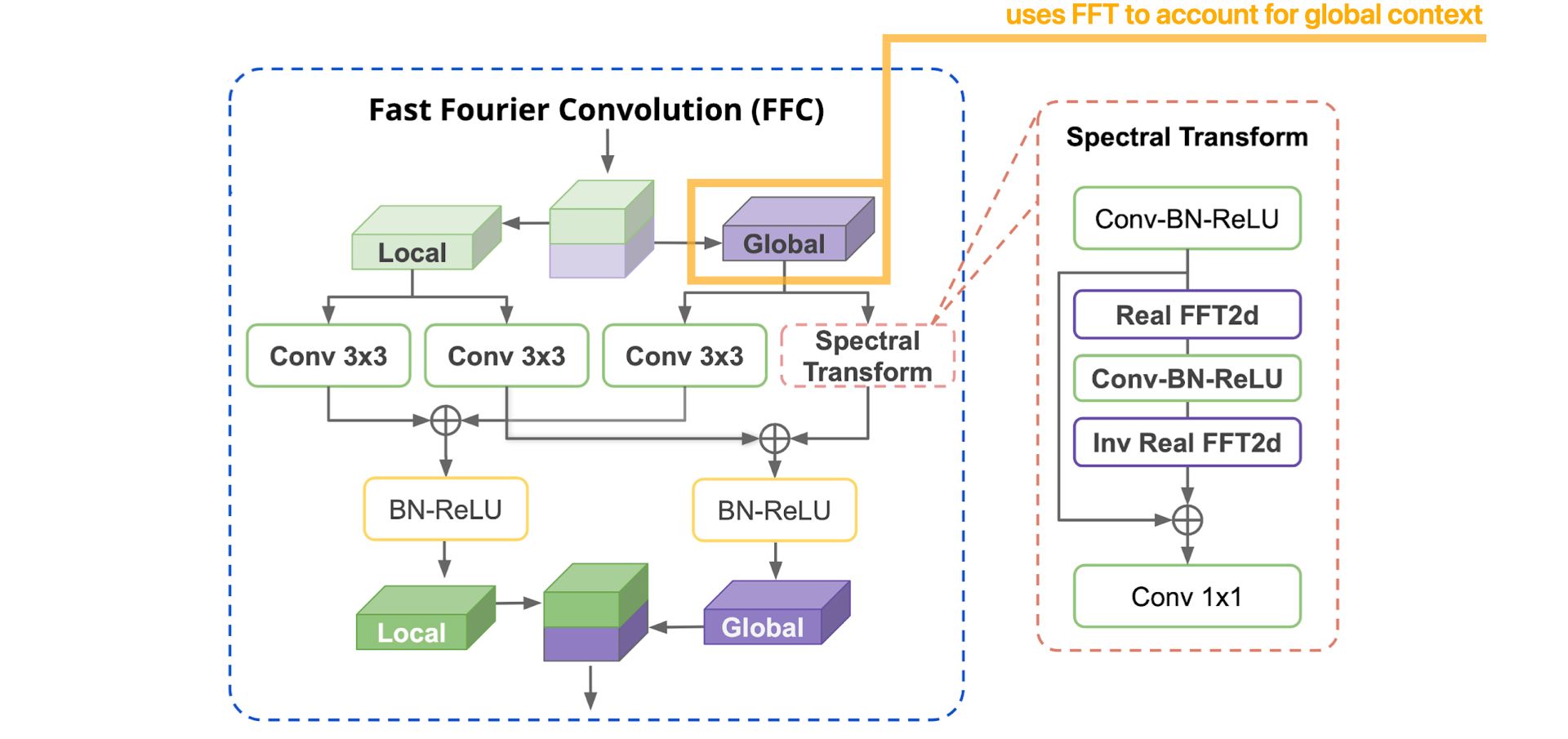
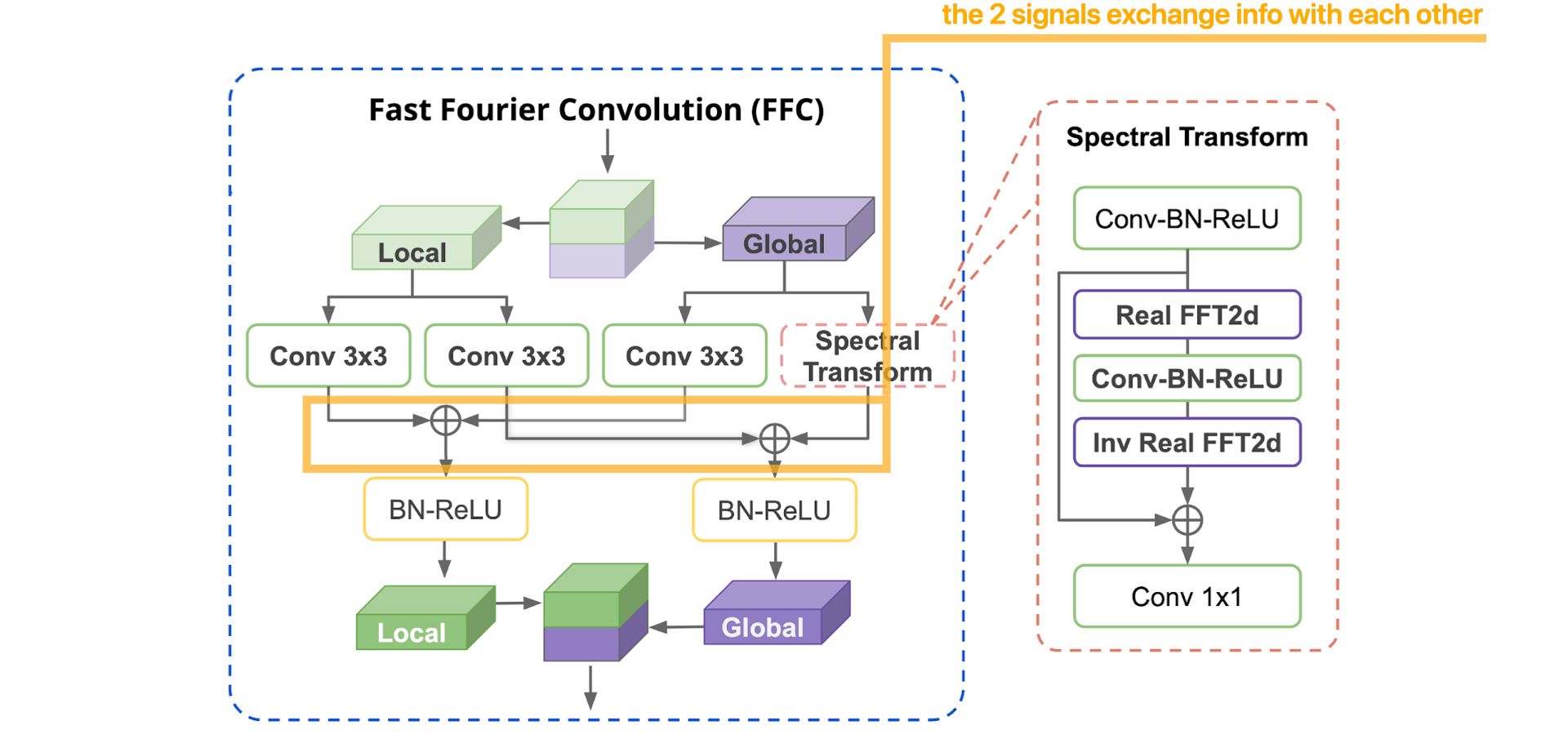


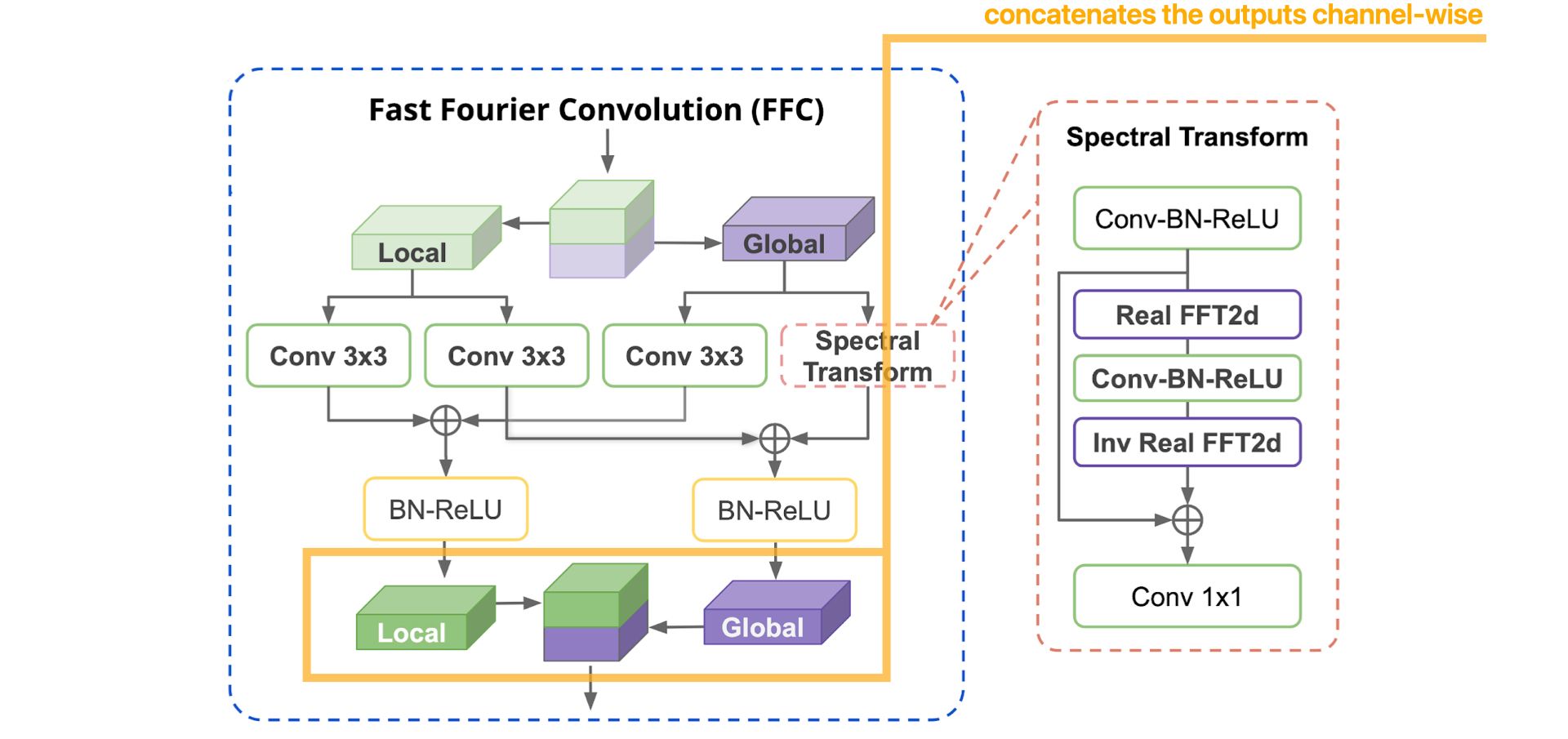
More details about the Spectral Transform :
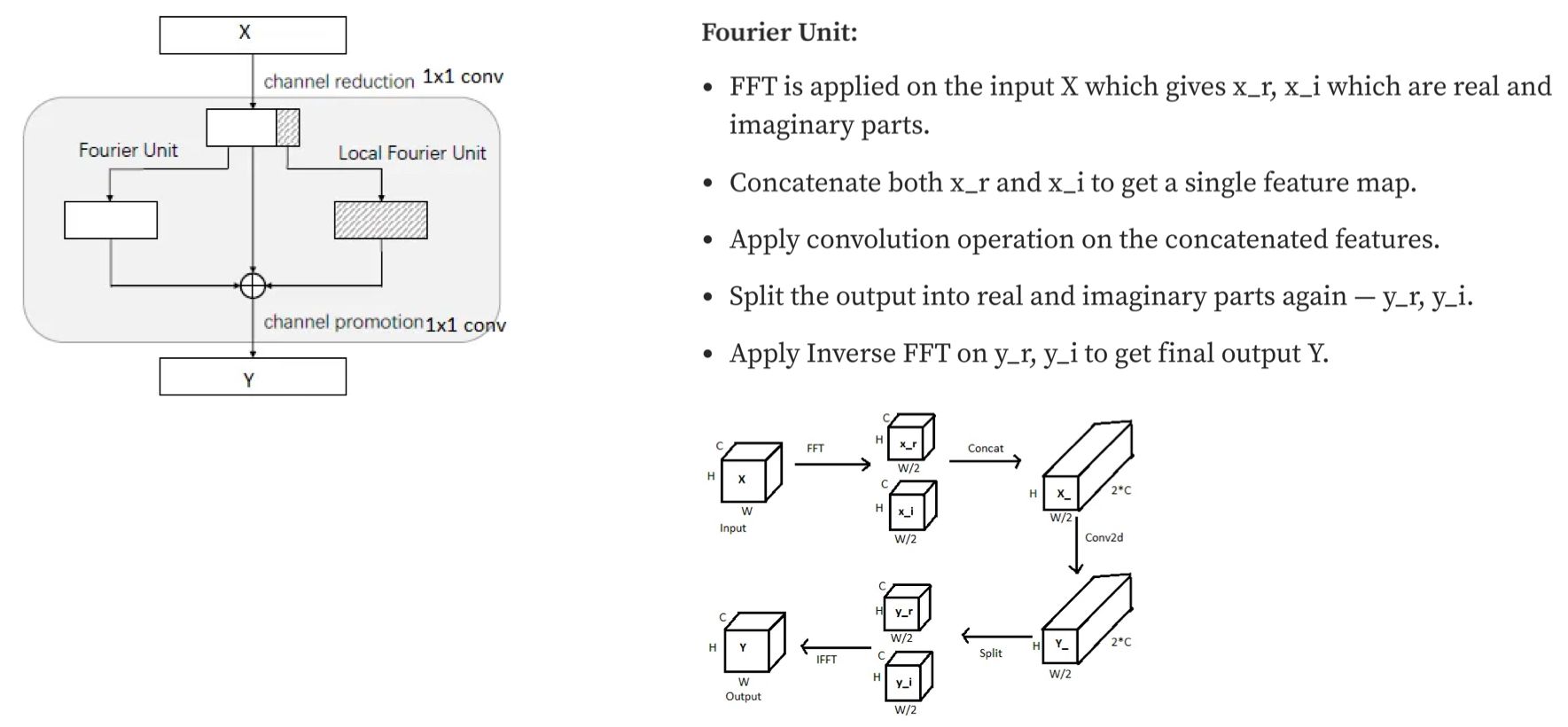
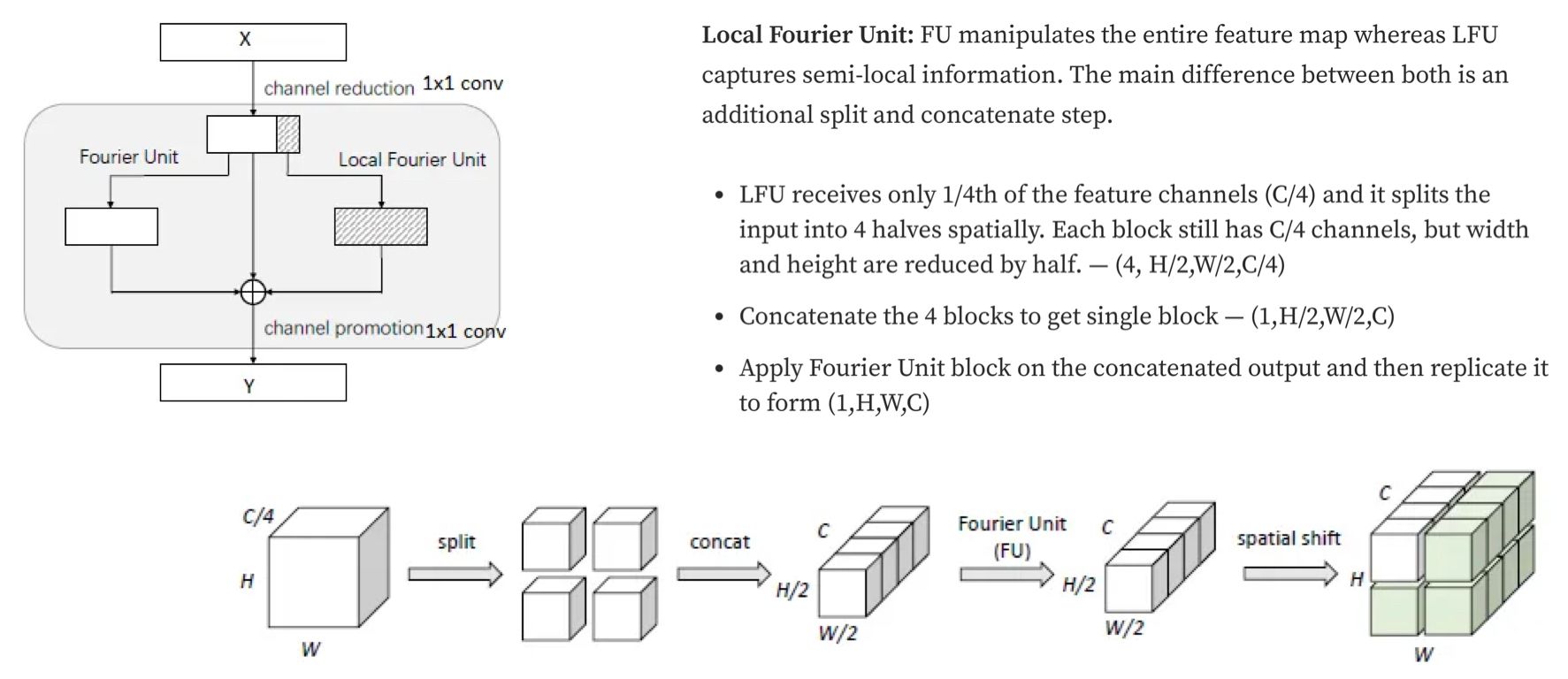
Loss functions
High Receptive Field Perceptual Loss
The Perceptual Loss (PL) is commonly used to evaluate the distance between the features computed by a trained base network
of the predicted images and the ground-truth images.
To better capture the global structure, LaMa uses the High Receptive Field PL, defined as follows :

Adversarial Loss
LaMa is trained with an adversarial loss, where the discriminator works on a local patch level and receives “fake” labels only for areas that intersect with the masks. Additionally, a PL
on the features of the discriminator is used.
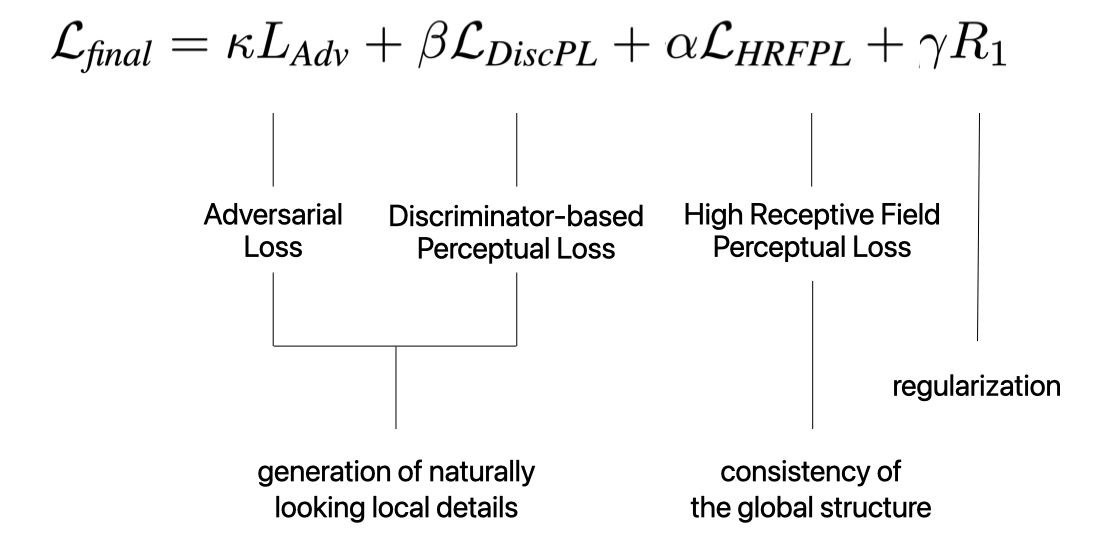
Final Loss
Masks generation
Base LaMa is trained with aggressively generated large masks that uses samples from polygonal chains dilated by a high random width and rectangles of arbitrary aspect ratios. The increased diversity of masks is beneficial for inpainting.
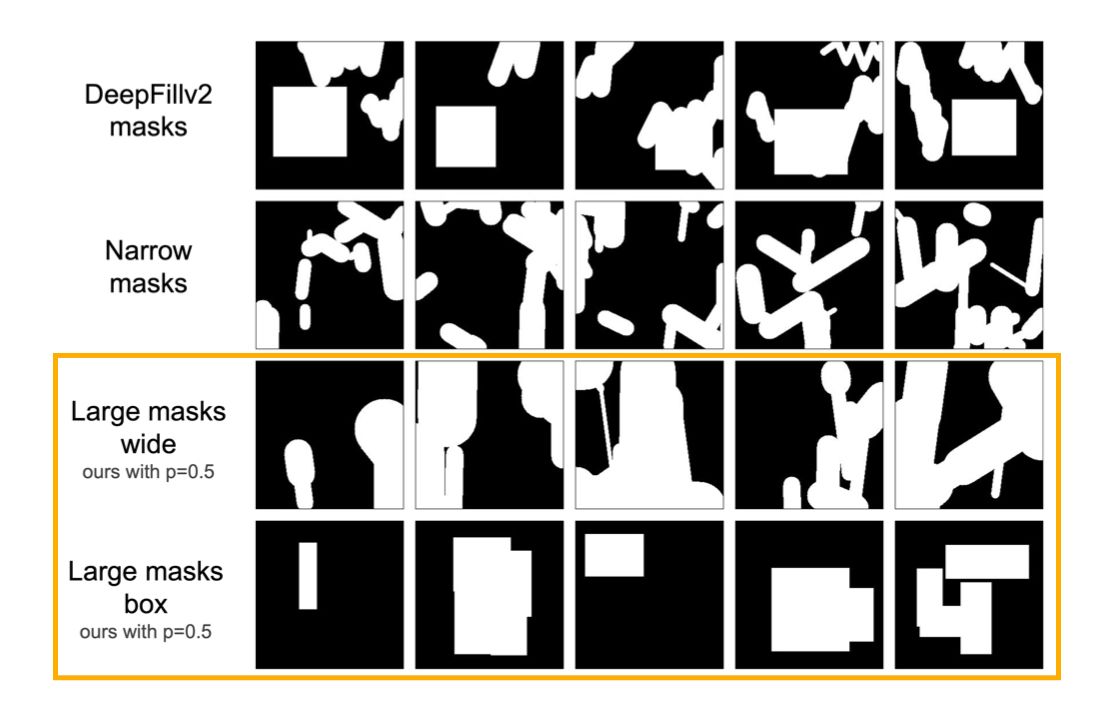
Unfortunately, the actual policy wasn't suited for the SkinGan project.
Instead, we generated diverse tattoo-like shapes on the skin.
Benchmarks, comparison with other inpainting models and some results
Datasets
It consists of patches from Places (scenes images) and CelebA-HQ (faces images).
Metrics
• FID (Frechet Inception Distance)
Distance in terms of statistic distribution between feature vectors of InceptionNet calculated for real and generated images
• LPIPS (Learned Perceptual Image Patch Similarity)
Similarity between the activations of two image patches for some predefined model
Benchmark (SOTA in Nov. 2021)

Some comparisons with other inpainting models

Some results concerning the SkinGAN project



A possible improvement to LaMa-Fourier :
Refinement for inpainting high resolution image
Inpainting networks often struggle to generate globally coherent structures at resolutions higher than those in their training set.

To address this issue, the authors propose a novel coarse-to-fine iterative refinement approach that optimizes feature maps using a multiscale loss.
By leveraging lower resolution predictions as guidance, the refinement process produces detailed high-resolution inpainting results while preserving the color and structure from the low-resolution predictions.
This method can be applied to any inpainting generative model.
Normally, an inpainting model has 3 parts in the architecture:
• f_front : encoder networks
• f_rear : decoder networks
• z : feature map
Here's an example :

Coase-to-fine

On the left, we have a pyramid of images with increasing resolutions. These correspond to the inputs for each iteration step of the fine-tuning process on the right. The smallest scale is approximately equal to the network's training resolution. At the lowest resolution, we perform a single forward pass through the entire inpainting model to obtain an initial inpainting prediction. We assume that the network performs best at the training resolution and use it as the foundation for guiding the inpainting structure at all scales.
In each iteration, we run a single forward pass through the "front" to generate an initial feature map, denoted as z. The rear part of the network processes z to generate an inpainting prediction. The prediction is then downscaled to match the resolution of the previous scale's result. An L1 loss is calculated between the masked inpainted regions and is minimized by updating z through backpropagation. This optimization process aims to generate a higher resolution prediction with similar characteristics to the previous scale. The final prediction, with the desired resolution, is obtained after all iterations.
Multiple featuremaps map (e.g. from skip-connections) instead of a single feature can be jointly optimized.
Benchmark
This table shows a performance comparison against recent inpainting approaches on 1,000 1024x1024 size images sampled from the Unsplash dataset.

This method demonstrates superior performance compared to reported state-of-the-art inpainting networks for medium and thick masks. However, it performs similarly to Big-LaMa for thin masks. It's important to note that while the refinement process yields higher quality results, it also requires significantly more time to process each image.
Here are some examples of inpainted images. The middle image shows the inpainted result without refinement, while the image on the right side represents the same image with refinement applied.